PRTF - Perry Rhodan Technik Forum
Das Viren-Imperium
- Anhänge -
(c) Michael Gebinoga Januar 2000
Naturwissenschaftliche Grundlagen
Die nachfolgend aufgeführten Themen und Theorien aus dem Bereich der Naturwissenschaften sind auf dem Stand des ausgehenden 20. Jahrhunderts. Einige der vorgestellten Theorien sind noch in der weiteren Entwicklung und es wurden erste, nachprüfbare Ableitungen gefunden.
Aufbau und Funktion von Viren
Beim Virenimperium sind Viren der Dreh- und Angelpunkt und
bedürfen deshalb einer kurzen Einführung.
Im Gegensatz zu Bakterien oder anderen Einzellern sind Viren nicht
als Lebewesen aufzufassen. Viren sind für sich nicht
lebensfähig, da sie keine Möglichkeit haben, komplexe
Nahrungsbestandteile in einfache Biomoleküle (z.B.
Aminosäuren oder Nucleotide) zu zerlegen, und diese für
ihre Vermehrung zu nutzen. Weiterhin können sie solche
vorliegenden, einfachen Grundbausteine nicht ohne Hilfe zur
Synthese neuer Proteine oder neuer Abschriften ihrer Erbinformation
nutzen. Wir haben es bei Viren mit molekularen Parasiten zu tun und
in der Tat gibt es für jede bekannte Lebensform auf der Erde
auch Viren, die diese Lebensform als Wirte nutzen (Bakterien,
Pflanzen, Insekten, Fische, Vögel, Säugetiere usw.). Die
Vermehrung ihres Genoms (Erbgut) ist nämlich der Hauptzweck
der Viren. Sie benutzen ihre jeweiligen Wirtsorganismen, um sich in
ihnen vermehren zu lassen und um ihre genetische Information in den
Wirten realisieren zu können.
Grundsätzlich bestehen Viren aus zwei Komponenten:
- Genetische Information aus RNA oder DNA
- Schutzhülle aus Proteinen und gegebenenfalls einige notwendige Enzyme
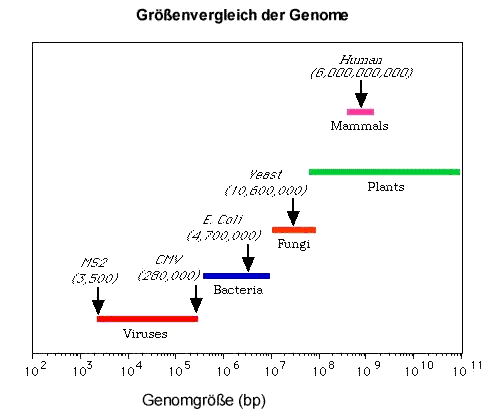Abbildung 1:
Größenvergleich verschiedener Genome von Organismen und
typische Vertreter (MS2: Bakteriophage; CMV: Cytomegalievirus; E.
coli: Darmbakterium).
Die genetische Information von Viren beinhaltet alle notwendigen Enzyme und Proteine, welche das Virus für seine Replikation und Verpackung benötigt. Mitunter gehören noch weitere Proteine zur Ausstattung dazu, die den Wirtsstoffwechsel insoweit beeinflussen, dass die Stoffwechselvorgänge des Wirts unterbunden werden, um die virusspezifischen Prozesse mit größtmöglicher Geschwindigkeit ablaufen zu lassen. Das Genom der Viren ist generell deutlich kleiner als das ihrer Wirte (siehe Abbildung 1 und Abbildung 2). Wir sehen, dass Viren eine Größe von etwas über 3000 Basenpaaren bis hin zu 300.000 Basenpaaren abdecken. Ein Basenpaar entspricht dabei einem Buchstaben des genetischen Alphabets. Während die kleineren Viren meistens nur ihre absolut lebensnotwendige genetische Grundausstattung "an Bord“ haben, können Viren mit größerem Genom auch eine Reihe von zusätzlichen Genen beherbergen. Viren bieten sich somit als Container und Transportbehälter für Gene an und werden in den modernen "Life-sciences“ auch entsprechend genutzt. Viren zeigen bei ihrem Zusammenbau ein sehr überraschendes Bild. Sie setzen sich nämlich von selbst aus den entsprechenden Vorstufen (Proteine und Nucleinsäuren) zu funktions- und infektionsfähigen Partikeln zusammen. Dieser Selbstzusammenbau wird als Self-assembly bezeichnet. Sobald die Ausgangsstoffe in hinreichender Konzentration vorliegen, kommt es zum spontanen Self-assembly. Dieser Prozeß läuft sehr schnell ab.
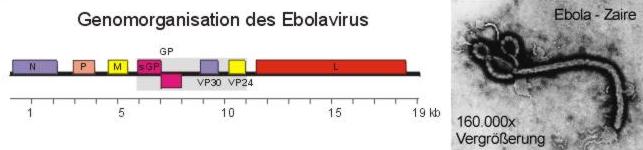
Abbildung 2:
Genomorganisation und elektronenmikroskopische Aufnahme des
Ebolavirus. Seine genetische Grundausstattung beträgt ca.
19.000 Nucleobasen, welche für seine Proteinausstattung
kodieren. Der größte Genabschnitt (von 11.5 - 18.5 kb)
kodiert für die virale RNA Polymerase.
Normale Viren verwenden hauptsächlich zwei Syntheseprozesse:
- DNA bzw. RNA Replikation durch entsprechende DNA oder RNA Polymerasen.
- Proteinbiosynthese durch den Translationsapparat (Ribosomen) ihrer Wirtszellen.
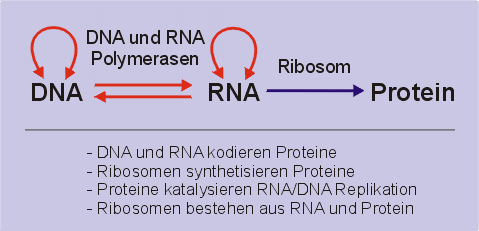
Ersterer (DNA/RNA Replikation) ist ein relativ einfacher
Prozeß, der mit einem oder wenigen Proteinen auskommt, die
die Replikation der ursprünglichen Nucleinsäure
katalysieren. Die entsprechenden Polymerasen werden durch das
Virusgenom kodiert. Beim zweiten Prozeß haben wir hingegen
einen der kompliziertesten Prozesse der Molekularbiologie
vorliegen. Bei der Translation wird die genetische Information, die
sich auf einem RNA Strang befindet, an einem Ribosom in ein Protein
übersetzt. Ein Virus nutzt immer den Translationsapparat
seines Wirts.
Das Ribosom selbst ist ein Multienzymkomplex aus ca. 50 Proteinen
und drei unterschiedlich großen Ribonucleinsäuren.
Weiterhin werden noch zusätzliche Proteine,
transfer-Nucleinsäuren (tRNA), Aminosäuren und die
eigentliche Boten-Nucleinsäure (mRNA) benötigt.
Ende der 90er Jahre wurden Experimente begonnen, bei denen versucht wird, mit einer Minimalausstattung die Translation zu gewährleisten. Dies macht Sinn, da der heutige Hochleistungstranslationsapparat das vorläufige Endergebnis einer Milliarden Jahre umfassenden Evolution ist. Es ist plausibel, dass die Translation mit einem deutlich verringerten Enzymapparat laufen kann und es ist durchaus möglich, dass ein radikal vereinfachter Translationsapparat entwickelt werden kann, der aber trotzdem hocheffizient ist.
Ein Punkt, der bei genauerer Betrachtung der viralen Lebensweise
ins Auge sticht, ist ihre unglaublich hohe Effizienz. Wir haben
hier molekulare Parasiten vor uns, die nur aus ein paar Proteinen
und etwas Nucleinsäure bestehen. Beispielsweise hat das
Ebolavirus ein Erbgut, welches 19.000 Nucleotide umfasst - das
Erbgut des Menschen umfasst über 3 Milliarden Nucleotide
(siehe Abbildung 2). Dennoch ist das Ebolavirus im Menschen
hochgradig effizient und führt in den meisten Fällen zum
Tode des Betroffenen. Aus diesem Grund sind Viren auch ein sehr
begehrtes Forschungsobjekt in einem Bereich, der als schwarze
Biologie bezeichnet wird (Biokampfstoffforschung). Beim Aufbau des
Ebolagenoms finden wir eine grau unterlegte Region, welche deutlich
variabler als der Rest des Genoms ist. Wir finden hier bei einer
Viruspopulation Nucleinsäuresequenzen, die leichte
Abweichungen untereinander aufweisen. Diese individuellen Viren
(und Nucleinsäuresequenzen) treten auch bei allen anderen
Viren auf und werden als Quasispezies bezeichnet.
Der Begriff wurde von Manfred Eigen eingeführt und gehört
heutzutage zu den Standardkonzepten der Evolutionstheorie.
Weiterhin können übergreifende Bereiche eine
entsprechende Information tragen, die als gesamtes Protein
exprimiert wird oder in Form mehrerer einzelner Proteine. Wenn wir
das Beispiel aus Abbildung 2 nehmen, könnte z.B. eine weitere
Information vom Bereich 3 kb bis 6 kb gehen, die unter bestimmten
Umständen freigesetzt wird. Bei Ebola findet sogar noch eine
interessantere Variante statt, jedoch würde eine
Erläuterung dieses Mechanismus an dieser Stelle zu weit
führen.
Theoretische Konzepte der molekularen Evolution
Bei den hier vorgestellten Konzepten aus dem Bereich der molekularen Evolution handelt es sich um Theorien und Gedankenansätze, die in der Schule um Manfred Eigen entwickelt wurden. Eine umfassende Einführung in die Theorie der Selbstorganisation biologischer Makromoleküle findet sich in einer Arbeit von Eigen aus dem Jahre 1971.
Quasispezies: Der Begriff einer Quasispezies
läßt sich am Beispiel eines RNA Virus sehr anschaulich
erklären. RNA Viren haben Genome aus RNA
(Ribonucleinsäure), wobei die RNA eine Kettenlänge von
ca. 4000 bis 20000 Nucleotide hat. Bei den längerkettigen
Viren handelt es sich um DNA Viren.
Abbildung 3: Bei den Sequenzen 1 bis 8 handelt es sich um Nachkommen einer Sequenz. Die neuen Sequenzen weisen alle Mutationen auf (rote Buchstaben). Nimmt man alle Sequenzen zusammen und schaut nach, an welcher Stelle welche Base am häufigsten erscheint, bekommt man die sogenannte Konsensussequenz. Diese Konsensussequenz kann - aber muß nicht - auch in der Quasispezies vertreten sein.
Bei der Replikation der RNA werden Kopien der ursprünglichen RNA hergestellt und ein Virus kann mehrere tausend Nachkommen haben. Nun ist der Kopierprozeß bei RNA Viren sehr fehleranfällig und ca. alle 1000 - 5000 Nucleotide wird statistisch ein Fehler eingebaut. Selbst wenn wir von 100 Virusgenomen ausgehen, die exakt dieselbe Sequenz haben, so haben wir nach wenigen Generationen eine Vielfalt von Sequenzen, die im MITTEL zwar noch der ursprünglichen Sequenz entspricht, jedoch mehrere Fehler (Mutationen) aufweist (siehe Abbildung 3). Dabei können sowohl Fehler auftauchen, die für das Virus tödlich sind, als auch Fehler, die dem Virus eine Resistenz gegen einige Medikamente verleihen, oder dem Virus die Möglichkeit geben, sich schneller zu vermehren. Genome, die nachteilige Fehler aufweisen werden ausgemerzt (Selektion), während die positiven Mutanten mehr Nachkommen erzeugen. Wir haben letztendlich also eine Population von Viren, deren Erbgut sich sehr stark ähnelt, aber nicht mehr identisch ist. Solche Populationen bezeichnet man als Quasispezies. HIV-1 ist ein Paradebeispiel für dieses Konzept.
Das Konzept der Quasispezies hat weitreichende Konsequenzen für die Evolution von Viren im speziellen, aber auch für die Evolution insgesamt. Für eine genauere Betrachtung dieses Konzeptes benötigt man zwei weitere Konzepte der molekularen Evolutionstheorie - den Sequenzraum und die Theorie der neutralen Netze. Hierbei werden die verschiedenen Nucleinsäuremutanten zueinander in Relation gesetzt und es ergeben sich daraus weitreichende Perspektiven.
Sequenzraum: Das Konzept des Sequenzraumes dient zur Versinnbildlichung der Anordnung und der Mutationsmöglichkeiten verschiedener, ähnlicher Sequenzen. Dabei entspricht die Dimensionalität des Sequenzraumes der Kettenlänge der Sequenz. Für eine Sequenz der Kettenlänge 3 benötigen wir einen dreidimensionalen Sequenzraum, wohingegen eine Sequenz der Kettenlänge 100 in einem hundertdimensionalen Raum abgebildet wird (siehe Abbildung 4).
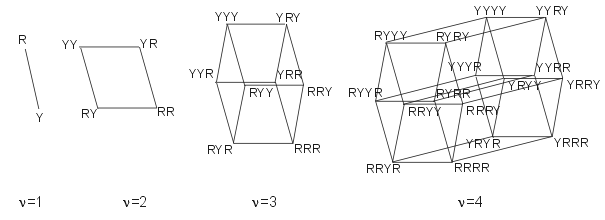Abbildung 4:
In dem Schaubild sind schematische Repräsentationen des
Sequenzraumkonzeptes für Kettenlängen von 1 bis 4
dargestellt. In diesem Beispiel wird von einem binären Code (Y
und R) der zugrundeliegenden Ketten ausgegangen. Es ist klar zu
sehen, dass die Konnektivität mit wachsender Kettenlänge
stark ansteigt. Jede Position entspricht dabei einer spezifischen
Sequenz und von dieser Sequenz kann man durch eine Mutation (R nach
Y oder vice versa) über einen Schritt zu der entsprechenden
Sequenz gelangen.
In einem realen Fall (Viruspopulation) wären die meisten Positionen nicht besetzt. Zum einen mangels Masse und zum anderen können bestimmte Positionen Mutationen versinnbildlichen, welche für das Virus tödlich sind. Dennoch besteht die prinzipielle Möglichkeit und falls eine entsprechende, noch unbesetzte Position mit einer entsprechend vorteilhaften Mutation übereinstimmt, so kann diese Position über mehrere Schritte relativ schnell realisiert werden, obwohl der Sequenzraum als solcher riesig groß werden kann.
Die Größe des Sequenzraums eines sehr kleinen RNA Strangs von 70 Nucleotiden errechnet sich nach folgender Formel:
Z = mn
Dabei ist m die Zahl der Möglichkeiten für die
Besetzung einer Position (im binären Code wäre m=2 und im
Nucleinsäurecode wäre m=4). Die Variable n entspricht hierbei der Kettenlänge der
jeweiligen Sequenz.
Für unser Beispiel der kleinen RNA von 70 Nucleotiden
Länge errechnen wir die Zahl der Position mit
Z = 1.4 x 1042 !!! Es ist leicht einzusehen, dass die
Zahl der Positionen im Sequenzraum für
Nucleinsäuresequenzen der üblichen Länge (ca. 1000
bis 5000 Nucleotide) die Zahl der vorkommenden Atome im Weltall
(ca. 1080) um Größenordnungen übersteigt
(überastronomisch groß).
Der Sequenzraum für das Genom des Ebolavirus (ca. 19000
Nucleotide) im ganzen, würde
1011439 Positionen umfassen!!!
Neutrale Netze: Bei der Theorie der neutralen Netze
handelt es sich um die Behandlung von dichten und verbundenen
Netzen in multidimensionalen Räumen. Der mathematische
Hintergrund der Theorie ist nicht trivial und geht von einem
graphentheoretischen Ansatz aus. Glücklicherweise sind die
Ergebnisse jedoch qualitativ verständlich zu machen, ohne das
man tief in die Mathematik einsteigen müßte. Mitte der
90er Jahren wurden an SGI Supercomputern theoretische
Untersuchungen des vollständigen Sequenzraumes von kurzen
Sequenzen durchgeführt*. Die Ergebnisse waren
überaus interessant. Bekanntermaßen falten sich
einzelsträngige RNA Sequenzen zu Gebilden, die nur
abschnittsweise der üblichen Doppelhelixstruktur von DNA
entsprechen. Es zeigte sich nun, dass auch und gerade bei Viren
unterschiedliche Sequenzen einer Quasispezies dennoch eine
ähnliche Struktur aufweisen. Treten nachteilige Mutationen
auf, so sind die sich daraus ergebenden Strukturen häufig
anders gefaltet, als die neutralen oder vorteilhaften
Mutanten.
Die neutralen Mutanten hingegen bilden ein engverwobenes Netzwerk
im Sequenzraum aus. Dabei gilt auch hier, dass bei realen
Populationen dieses Netzwerk nur zum allerkleinsten Teil durch
existierenden Sequenzen aufgefüllt ist.
Die möglichen Konsequenzen aus diesem Aspekt sind
ausgesprochen weitreichend. Man kann vermuten,
dass eine normale Viruspopulation nur einen sehr kleinen Teil
seines neutralen Netzes im Sequenzraum besetzt. Wächst diese
Population an, so werden weitere Positionen besetzt und darunter
können auch welche sein, die dem Virus Resistenzen gegen
verschiedene Medikamente bieten. Es ist folglich von
Interesse,
darauf zu achten, dass bei Infektionen das Wachstum der
Viruspopulation eingedämmt wird, da eine größere
Population einfach eine bessere Chance hat, Mutanten gegen
bestehende Medikamente auszubilden.
Ein weiterer Punkt ist der Einsatz von Impfstoffen
(abgeschwächte Viren). Impfstoffe führen zu einer
Immunisierung des Körpers gegen ein Virus. Der Impfstoff ist
häufig eine abgeschwächte Form dieses Virus und nicht
krankheitserregend. Es zeigte sich jedoch, dass bei einer Impfung
die schwachen Impfviren sich vermehren und mutieren. Dabei kommt es
dann innerhalb von 8 - 24 Stunden nach der Impfung zu
Rückmutationen und letztendlich zu einer vollständigen
Rückverwandlung der Impfviren in hochvirulente Erreger! Der
Zeitvorsprung den das Immunsystem jedoch hat, reicht aus, um damit
fertigzuwerden.
Die Schnelligkeit, mit der der Prozeß der Rückmutation
vonstatten geht, wird durch die Theorie der Neutralen Netze
erklärt.
Physikalische und informationstechnische Beschränkungen
Verwendete Abkürzungen:
h: Plancksches Wirkungsquantum
E: Energie (in Joule (J))
t: Zeit (in Sekunden (s))
p: Impuls (in kg.m/s)
m: Masse (in kg)
v: Geschwindigkeit (in m/s)
Heisenbergsche Unschärferelation: Die Heisenbergsche
Unschärferelation gibt eine grundsätzliche Schranke
für die Genauigkeit an, mit der zwei physikalische
Größen gleichzeitig gemessen werden können. Diese
Messunschärfe hat nichts mit apparativen Ungenauigkeiten zu
tun, sondern ist naturgegeben. Beispiele für diese Beziehung
sind die Energie-Zeit-Unschärfe (DE .Dt >= h) und die
Ort-Impuls-Unschärfe
(Dx .Dp >= h). Das
heißt, wenn für eine Energiemessung nur die ZeitDt zur Verfügung steht, dann kann die Energie
nicht genauer alsDE gemessen werden. Bei der
Ort-Impuls-Unschärfe kann den Ort x und den
Impuls p (p = mv) eines Teilchens nicht gleichzeitig beliebig
genau festlegen.
Die Heisenbergsche Unschärferelation erlaubt beispielsweise auch das virtuelle Auftreten eines einzelnen Photons nach einer Elektron-Positron Paarvernichtung. Dieser Prozeß wäre zwar nach dem Impulserhaltungssatz verboten (es müßten mindestens zwei Photonen entstehen), aber er kann innerhalb der Grenzen der Energie-Zeit-Unschärfe auftreten. Aufgrund der sehr hohen Energie des einzelnen Photons (als AbweichungDE von E), ist folglich seine Lebensdauer (als AbweichungDt von t = 0) entsprechend gering und es zerstrahlt sofort wieder, um z.B. in ein Quark-Antiquark-Paar überzugehen.
Halte-Problem: Alan Turing war einer der größten Pioniere im Computerwesen und in der Kryptographie des 20. Jahrhunderts. Bei seinen Arbeiten über die Berechenbarkeit von Problemen stieß er auch auf das sogenannte Halte-Problem. Ein beliebiger Computer kann so lange kein Ergebnis erzielen, bis er seine Berechnungen in irgendeiner Weise gestoppt hat. Das sogenannte Halte-Problem ist die Frage, ob es ein allgemeines Verfahren gibt, welches uns vorhersagen kann, ob ein bestimmtes Programm nach einer endlichen Anzahl von Schritten anhalten wird. Alan Turing zeigte 1936 n.Chr. auf, daß es prinzipiell nicht möglich ist, ein solches Verfahren anzugeben.
Gödelsche Unvollständigkeitssatz: Der
Mathematiker Kurt Gödel hat im 20. Jahrhundert entscheidende
Schlußfolgerungen über das Wesen der Mathematik und das
Verständnis formaler Systeme gezogen. Gödel befaßte
sich damit, Axiome zu bestimmen, die als Grundlage für die
gesamte Mathematik dienen können.
Bei seinen Arbeiten konnte Gödel beweisen, daß die
gesamte Mathematik nicht konsistent ist und es auch nicht sein
kann. Er zeigte auf, daß es innerhalb eines beliebigen
axiomatischen Systems unweigerlich Sätze gibt, die weder
bewiesen noch widerlegt werden können. In vereinfachter Form
lautet Gödels Unvollständigkeitssatz:
Jeder widerspruchsfreie Kalkül, der es erlaubt, von den natürlichen Zahlen zu sprechen, der also die elementare Arithmetik umfaßt, enthält unendlich viele Aussagen, die in diesem Kalkül weder bewiesen noch widerlegt werden können.
Wir haben hier also eine unentscheidbare Aussage vorliegen. Gödels Beweis ist somit das erste mathematische Beispiel dafür, daß es nur außerhalb eines nichttrivialen Universums möglich ist, dieses vollständig zu beschreiben. Gödels Unvollständigkeitstheorem wird häufig als die wichtigste mathematische Theorie bezeichnet.
* Bei den Sequenzen handelte es sich um Ketten aus zwei Buchstaben des genetischen Alphabets (C und G) der Kettenlänge 30. Nach der Formel Z = mn ergeben sich daraus etwa eine Milliarde Sequenzen, die thermodynamisch berechnet werden mußten.
|
weiter zu: |
|||
|
Geschichte des
Viren-Imperiums |
|||
